- 参考
- CNFs是对传统(离散)归一化流思想的一次优雅的升华
- 核心引擎:常微分方程 (ODE)
- 如何求解:欧拉法(Euler's Method)
- CNF的训练与损失函数
参考
https://gemini.google.com/app/a5a75c33b55945bd
https://zhuanlan.zhihu.com/p/685921518
CNFs是对传统(离散)归一化流思想的一次优雅的升华
为了理解CNF,我们先回忆一下标准的归一化流(NF):
标准NF:像是在走楼梯。我们通过一系列离散的、独立的函数变换 \(f₁, f₂, ..., fₖ\),一步一步地将简单的基础分布扭曲成复杂的目标分布。每一步都是一次跳跃。
连续NF (CNF):现在,想象一下我们不走楼acie,而是走在一个平滑的斜坡上。我们不再是一步步跳跃,而是以一种连续、平滑的方式,将基础分布无缝地“流动”到目标分布。
CNF就是用一个平滑的“斜坡”代替了原来的一节节“楼梯”,从而实现了更灵活、更平滑的变换。
核心引擎:常微分方程 (ODE)
这个平滑的“流动”过程,在数学上是用一个常微分方程(Ordinary Differential Equation, ODE)来描述的。公式:
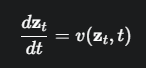
\(t\): 代表连续的时间,通常我们设定 \(t\) 从0到1。可以把它想象成变换的“进度条”。
\(t=0\) 时,我们处于初始的简单高斯分布。
\(t=1\) 时,我们希望已经到达了复杂的目标数据分布。
\(z_t\): 代表一个数据点在时间 \(t\) 时的状态或位置。随着 \(t\) 从0到1变化,\(z_t\) 会划出一条连续的轨迹。
\(dz_t/dt\): 这是微积分中的导数,代表了数据点 \(z_t\) 在 \(t\) 时刻的瞬时速度(变化的方向和快慢)。
\(v(z_t, t)\): 这是整个CNF的“大脑”,一个向量场(Vector Field)。
它通常由一个大型神经网络来表示。
它的作用:对于空间中的任何一个点 \(z_t\) 和任何一个时间 t,这个神经网络 \(v\) 都能给出一个速度向量。
绝佳的比喻:你可以把整个数据空间想象成一条河流。\(v(z, t)\) 就是描述这条河在任何位置、任何时间的水流速度和方向的地图。我们的数据点 \(z_t\) 就像是河里的一片叶子,它会跟随水流漂动。
这个ODE公式的意义就是:数据点在任意时刻的运动轨迹,完全由一个神经网络 v 所定义的动态向量场来决定。 模型的任务,就是学习出这个能够将简单分布“漂流”到复杂分布的“水流图”。
如何求解:欧拉法(Euler's Method)
这个ODE给了我们“速度地图”(动态向量场),但没有直接给出“运动轨迹”。为了找出从 z₀ 到 z₁ 的完整路径,我们需要“求解”这个ODE。
由于v是一个复杂的神经网络,我们无法得到解析解,只能使用数值方法来近似求解。最简单的方法就是您截图中提到的欧拉法。
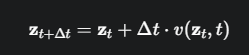
这个公式非常直观,完全符合我们的物理直觉:
\(未来的位置 = 当前的位置 + 一小段时间 × 当前的速度\)
我们把总时间 [0, 1] 切分成 \(N\) 个微小的步长 \(Δt\)。
从 \(z₀\) 开始,我们用神经网络 \(v\) 查出 \(z₀\) 处的速度 \(v(z₀, 0)\)。
我们沿着这个速度方向走一小步 \(Δt\),得到 \(z_{Δt}\)。
然后我们再用 \(v\) 查出 \(z_{Δt}\) 处的新速度,再走一小步...
如此反复 \(N\) 次,我们就近似地描绘出了从 \(z₀\) 到 \(z₁\) 的整条平滑轨迹。
CNF的训练与损失函数
和标准NF一样,CNF的训练目标也是最大化数据的对数似然。但计算 \(log p(x)\) 的方式变了。
在标准NF中,\(log p(x)\) 的计算需要累加雅可比行列式的对数:\(Σ log|det(J)|\)。计算行列式非常耗时。
在CNF中,数学家们证明了一个惊人的结果:这个累加项变成了一个积分项,并且被求和的项从行列式(determinant)变成了迹(trace)。
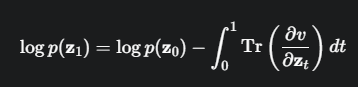
迹 (Trace):矩阵主对角线元素的和。计算“迹”比计算“行列式”在计算上快几个数量级!
这带来了巨大的优势:CNF摆脱了标准NF中计算成本高昂的行列式,使得模型可以扩展到非常高的维度。
所以,CNF的损失函数仍然是负对数似然,但其中的 log p(x) 是用上面这个迹的积分公式来计算的(这个积分也需要用数值方法近似)。
模型通过最小化这个损失,来学习那个能描绘数据真实“流向”的神经网络 v。
优点:
变换是连续和可逆的,表达能力更强。
参数共享:模型只有一个神经网络 v,而不是K个独立的层,内存效率高。
计算高效的似然变化:用“迹”代替了“行列式”,解决了标准NF的一个核心计算瓶颈。
缺点:
推理和训练速度慢:为了求解ODE,需要反复调用神经网络v成百上千次,这使得单次前向/反向传播非常耗时。
