设备接入方式日志
一、同一网段接入
当控制机与中心网管服务器处于同一网段时,设备网线连接正常且上电后,网管会自动搜索控制机,完成注册并分配 IP。后续只需等待控制机激活重启即可。
二、不同网段接入
此情况下无法自动搜索设备,需按以下步骤操作:
- 通过控制机显示屏查看其 IP(初始 IP 为 192.168.0.1,或为 DHCP 分配的 IP);
- 访问该 IP 进入控制机 Web 界面(需先将控制机恢复出厂设置);
- 在 “网络信息配置” 中修改设备 IP、网关、子网掩码;若设备为 jielink 模式,还需配置 NMS IP(即网管服务器所在电脑的 IP);
- 保存配置后,设备将注册到运维平台。
三、特殊情况接入(屏幕无法正常显示且与网关不在同一网段)
- 将控制机外网接口与电脑连接,尝试 ping 101.102.103.1;
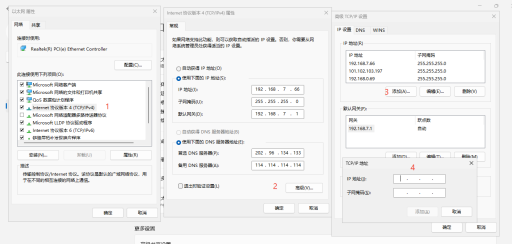
- 若无法 ping 通,在电脑的 “网络 Internet - 高级网络设置 - 以太网 - 编辑 - Internet 协议版本 4” 中添加 IP 地址;
![]()
- ping 通后,通过 ssh 连接到下位机,进入 JSQ1112 目录(执行命令:cd /opt/jsst/product/JSQ1112),再执行./web_start.sh 打开内置页面;
- 在 Web 端打开 101.102.103.1,进入 “车场控制机” 界面,修改 IP 地址和 NMS IP。
结论 :
在设备与网管不同网段且IP未知时,解决核心是通过配置同网段 IP 建立数据链路层连通性 —— 这是实现 ping 测试、SSH 连接等操作的基础。由此可见,遇网络类问题,应先排查链路层连通性(如网段匹配),为后续操作扫清基础障碍。