1、准备Google账号
登录网址https://colab.research.google.com/notebooks/welcome.ipynb
2、点击黄色Colab标识,进入Google Drive
点击目录 My Drive,创建文件夹Colab_test_by_zyn
3、进入文件夹,点击鼠标右键,点击Googel Colaboratory。如果没有,点击更多,点击 关联更多应用,搜索并下载Googel Colaboratory。
4、下载Biomu
!pip install bioemu
5、挂载云盘:
from google.colab import drivedrive.mount('/content/drive')
6、检查GPU
gpu_info = !nvidia-smigpu_info = '\n'.join(gpu_info)if gpu_info.find('failed') >= 0:print('Not connected to a GPU')else:print(gpu_info)
7、开始采样结构:
from bioemu.sample import main as sample# 设置输出路径(此处保存到云盘中的文件夹,可修改) output_path = '/content/drive/MyDrive/bioemu_test_output_CVC4'sample(sequence='...', #蛋白序列 num_samples=10, # 生成 10 个样本 output_dir=output_path # 输出目录 )

8、查看输出的结构文件
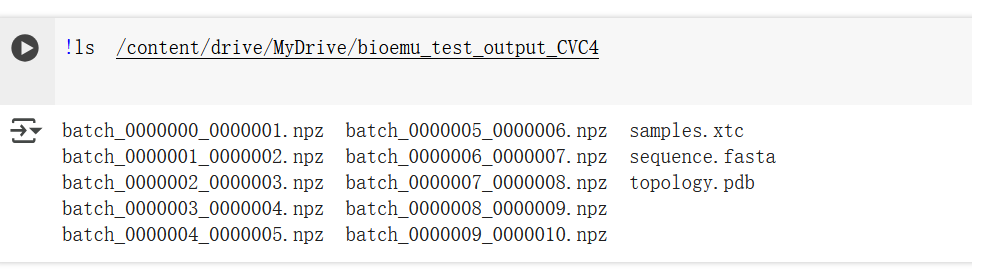
!ls /content/drive/MyDrive/bioemu_test_output
|
文件名 |
含义 |
|---|---|
|
batch_000000X_000000Y.npz(共10个) |
每一批采样结果,.npz 是 NumPy 的压缩格式,里面保存了采样得到的结构坐标、自由能等信息。你一共采样了10次(num_samples=10)。 |
|
samples.xtc |
一个 .xtc 文件(GROMACS 的轨迹格式),用于可视化所有采样结果的动态变化(例如用 VMD、PyMOL、MDTraj 可播放采样结构轨迹)。 |
|
sequence.fasta |
保存了你输入的蛋白质序列,标准 FASTA 格式。 |
|
topology.pdb |
一个结构拓扑文件,提供 backbone 拓扑结构,用于配合 samples.xtc 进行可视化。 |
9、批量保存为PDB文件
#全是A氨基酸import numpy as npimport osoutput_dir = '/content/drive/MyDrive/bioemu_test_output_CVC4'for i in range(10):npz_path = os.path.join(output_dir, f'batch_{i:07d}_{i+1:07d}.npz')with np.load(npz_path, allow_pickle=True) as data:coords = data['pos'][0]pdb_lines = []for j, (x, y, z) in enumerate(coords):atom_line = (f"ATOM {j+1:5d} CA ALA A{j+1:4d} "f"{x:8.3f}{y:8.3f}{z:8.3f} 1.00 0.00 C")pdb_lines.append(atom_line)pdb_lines.append("TER")pdb_lines.append("END")pdb_str = "\n".join(pdb_lines)with open(os.path.join(output_dir, f'sample_{i}.pdb'), 'w') as f:f.write(pdb_str)
#真实序列import numpy as npimport osaa_1to3 = {'A': 'ALA', 'R': 'ARG', 'N': 'ASN', 'D': 'ASP', 'C': 'CYS','E': 'GLU', 'Q': 'GLN', 'G': 'GLY', 'H': 'HIS', 'I': 'ILE','L': 'LEU', 'K': 'LYS', 'M': 'MET', 'F': 'PHE', 'P': 'PRO','S': 'SER', 'T': 'THR', 'W': 'TRP', 'Y': 'TYR', 'V': 'VAL'}output_dir = '/content/drive/MyDrive/bioemu_test_output_CVC4'for i in range(10):npz_path = os.path.join(output_dir, f'batch_{i:07d}_{i+1:07d}.npz')with np.load(npz_path, allow_pickle=True) as data:coords = data['pos'][0]seq = data['sequence']if isinstance(seq, np.ndarray):seq = seq.item()if isinstance(seq, bytes):seq = seq.decode()pdb_lines = []for j, (x, y, z) in enumerate(coords):aa_one = seq[j]aa_three = aa_1to3.get(aa_one, 'UNK')atom_line = (f"ATOM {j+1:5d} CA {aa_three} A{j+1:4d} "f"{x:8.3f}{y:8.3f}{z:8.3f} 1.00 0.00 C")pdb_lines.append(atom_line)pdb_lines.append("TER")pdb_lines.append("END")pdb_str = "\n".join(pdb_lines)with open(os.path.join(output_dir, f'sample_{i}.pdb'), 'w') as f:f.write(pdb_str)
10、下载PDB文件
from google.colab import filesimport timefor i in range(10):filepath = f'/content/drive/MyDrive/bioemu_test_output/sample_{i}.pdb'files.download(filepath)time.sleep(1) # 等待1秒,避免下载冲突或浏览器阻塞
11、下载拓扑结构文件和轨迹文件
from google.colab import filesfiles.download('/content/drive/MyDrive/bioemu_test_output/topology.pdb')files.download('/content/drive/MyDrive/bioemu_test_output/samples.xtc')
12、可视化所有结构变化轨迹(Pymol)
load topology.pdb
load_traj samples.xtc
cmd.set("movie_fps", 10)
cmd.movie.produce("轨迹.mp4", mode="movie")
注意:
1、感叹号!表示你要运行的是一个Linux/终端命令(shell命令),而不是Python代码。
2、程序会自动排除物理上不合理的结构(比如链断裂或空间冲突),所以实际生成的结构数可能少于你要求的数量。如果你想保留所有结构(包括不合理的),可以加上这个参数:
--filter_samples=False
3、目前这个代码只支持单体蛋白质(单条氨基酸链的蛋白)。多聚体(多个链组合)虽然可以试试链接,但作者说实验效果不好。
