SBC-T113产品特性:
-
采用Allwinner公司Cortex-A7双核T113-i处理器,运行最高速度为1.2GHZ;
-
内置64-bit XuanTie C906 RISC-V协处理器;
-
支持JPEG/MJPEG视频编码,最大分辨率1080p@60fps;支持多格式1080P@60fps视频解码 (H.265,H.264, MPEG-1/2/4);
-
支持RGB666/LVDS/MIPI-DSI,分辨率最高1920x1080;
-
支持512-1G Bytes DDR3 SDRAM;
-
支持SPI NAND存储和启动(默认:256MB;最大1GB)或者EMMC启动(默认:4GB,最大32GB);
-
支持四路USB2.0 HOST;
-
支持六路RS232通信;
-
支持双路CAN BUS通信(隔离);
-
支持双路以太网,一路10/100M;一路10/100/1000M;
-
稳定的操作系统的支持,可预装Ubuntu20.04/LINUX 5.4 Preempt/Tina5.0;
-
标准3.5寸主板, 尺寸为:146*102MM;
SBC-T113功能评估图:

1. 如何适配自己的开发板
本章节重点是说明如何把Tina系统(openwrt)适配到自己的开发板上。如需添加自己的产品,要关注以下两个目录,一个是主板的内核dts相关配置文件保存的目录,我们暂时叫它设备目录。另外一个是配置openwrt编译的相关文件。根据您选择的处理器和主板名字不同,他们存在的目录也不相同。
例如:以盈鹏飞嵌入式SBC-T113I这个平台为例,该平台是以全志T113i作为主处理器,产品名字是SBC-T113I,因为我们要适配的产品是NAND启动的,所以我们把产品名字命名为sbc_t113i_nand,那么保存内核dts相关配置配置目录:
SDK_ROOT/device/config/chips/t113_i/configs/sbc_t113i_nand
SDK_ROOT表示的是TinaSDK所在的根目录
保存openwrt的配置文件是在如下目录:
SDK_ROOT/openwrt/target/t113_i/t113_i-sbc_t113i_nand
我们先查看设备配置目录下的内容:

我们再查看openwrt的配置文件所在目录的内容:
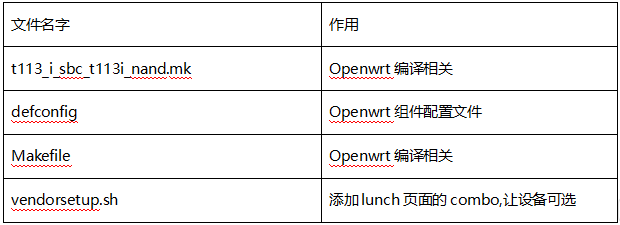
以上文件修改完成后,即可进行编译。那么这些文件是如何来的呢?以下章节我们进行说明。
2. 以全志官方的t113i平台evb1_auto_nand作为基础创建配置
SDK代码中通常会有一些针对全志官方板子适配的例子,例如针对于t113i平台的设备配置文件在SDK_ROOT/device/config/chips/t113_i/configs下有evb1_auto或者evb1_auto_nand两个目录,他们就是全志官方板子适配的例子。evb1_auto目录保存的是针对emmc启动的相关配置,evb1_auto_nand目录保存的是nand启动的相关配置。
在device/config/chips/t113/configs下复制一份evb1_auto_nand并重命名为sbc_t113i_nand:
cp -rf evb1_auto_nand/ sbc_t113i_nand
openwrt的配置文件在SDK_ROOT/openwrt/target/t113_i,这个目录下也有对应全志官方板子的适配文件,针对evb1_auto_nand的配置文件保存t113_i-evb1_auto_nand目录,
因此我们复制t113_i-evb1_auto_nand并重命名为t113_i-sbc_t113i_nand
cp -rf t113_i-evb1_auto_nand/ t113_i-sbc_t113i_nand
3. 进行设备文件的适配
BoardConfig.mk/env.cfg/sys_partiton.fex/board.dts/sys_config.fex/uboot-board.dts这几个文件是设备文件。一般来说,首先适配的主板的终端串口,然后内核dts适配主板(gpio分配),这里我们重点先说明如何修改主板的终端串口,有了终端串口就可以知道内核的运行状态,为以后适配内核打基础。因为终端串口涉及到u-boot启动阶段,也涉及到内核启动阶段,因此,终端串口的修改要修改u-boot的编译配置文件,也需要修改内核的配置文件,另外,还需要修改env.cfg/board.dts/sys_config.fex三个文件。
4. sbc-t113主板的串口IO分配
盈鹏飞嵌入式SBC-T113主板的终端串口连接的串口为UART0,所以我们使用UART0作为uboot和kernel串口,所以我们需要进行修改

查看手册原理图可知UART0使用PE2和PE3的func6
修改boot0串口
修改sys_config.fex即可修改boot0串口,路径在device/config/chips/t113_i/configs/sbc_t113i_nand,修改前:
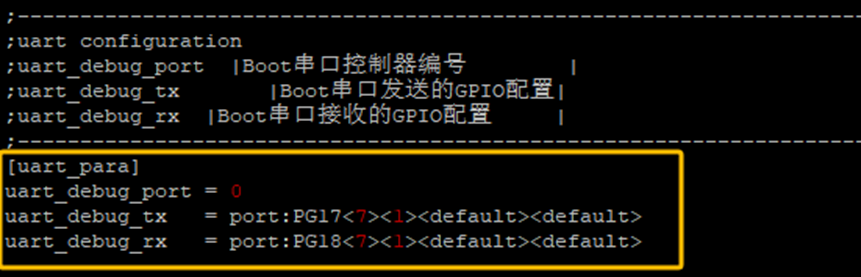
修改后:
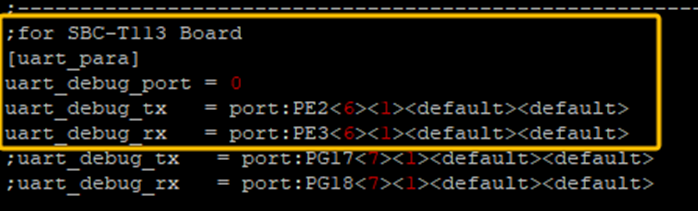
总结:使用的串口号填到uart_debug_port = 后面
使用的tx rx引脚号填到port后面,紧跟的第一个尖括号填对应功能为func功能号
5. 修改uboot串口
查看device/config/chips/t113_i/configs/sbc_t113i_nand目录下面的BoardConfig.mk文件
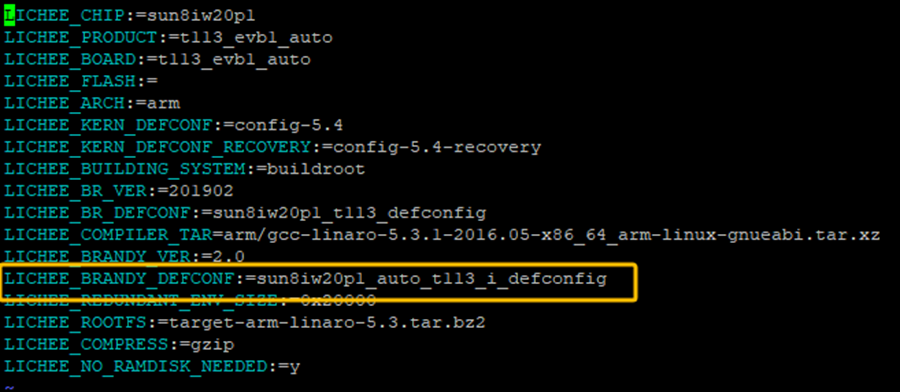
可以看到BRANDY_DECONF是指向sun8iw20p1_auto_t113_i_defconfig这个配置文件,这个配置文件中,有涉及到终端串口的配置,先查看该配置(该配置文件在SDK_ROOT/lichee/brandy-2.0/u-boot-2018/configs目录):
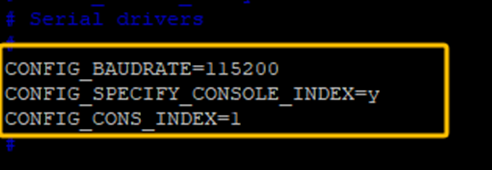
我们是使用UART0作为终端串口,所以该配置是正确的,不需要更改。
注意:CONFIG_CONS_INDEX = 串口号+1
例如本例中我们使用UART2,那么这里就要填3
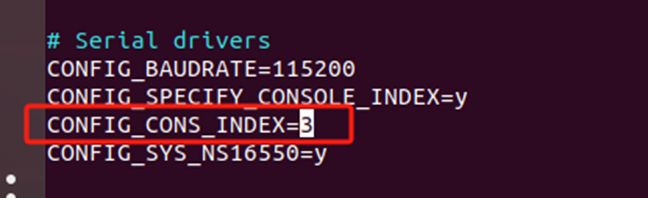
6. 修改Linux Kernel串口
在SDK_ROOT/device/config/chips/t113_i/configs/sbc_t113i_nand/linux-5.4目录下,存放board.dts文件是内核的设备树文件,先修改该文件让终端串口使能。注意SBC-T113是使用的PE2/PE3这两个GPIO作为UART0的,所以,务必要把uart0_pins_a和uart0_pins_b填写正确。

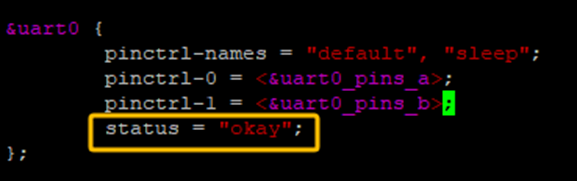
修改对应uart0的status为okay;
另外,还需要修改env.cfg文件,因为该文件中存放了内核启动的环境变量
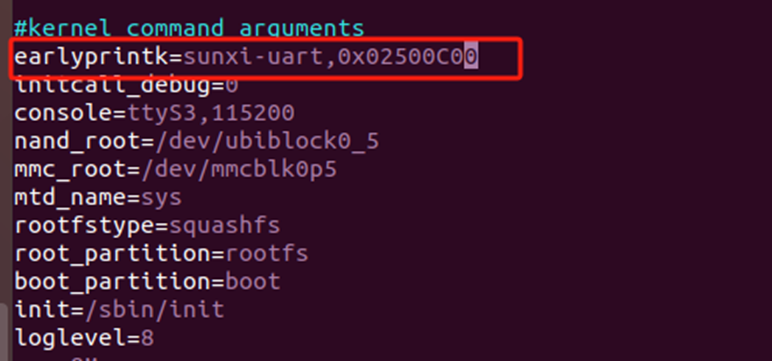
earlyprintk变量指定了内核日志打印的设备,第一个参数为对应设备,第二个参数设备地址,console指定了串口和波特率。
设备地址通过查看t113-i_user_manual手册中的Memory Mapping可确认

例如本例使用UART0的地址是0x2500000,那么修改env.cfg文件如下:
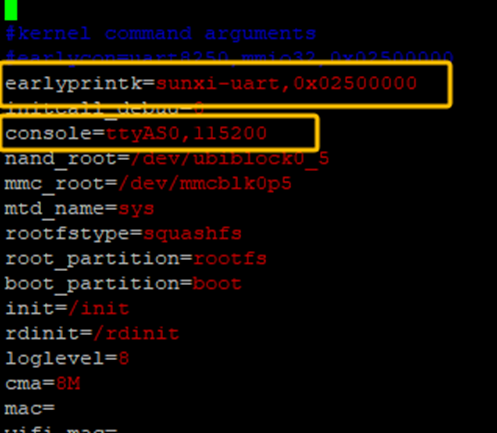
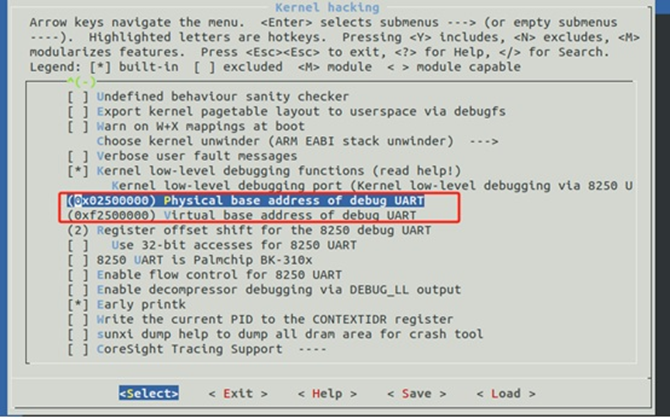
最后,还需要修改Kernel的配置文件,通过make kernel_menuconfig指令配置内核,找到kernel hacking->Kernellow-level debugging functions,修改寄存器地址:
7. 进行openwrt适配
进入SDK_ROOT/openwrt/target/t113_i下面的t113_i-sbc_t113i_nand目录,将t113_i_evb1_auto_nand.mk文件进行重命名为t113_i_sbc_t113i_nand.mk
mv t113_i_evb1_auto_nand.mk t113_i_sbc_t113i_nand.mk
然后编辑t113_i_sbc_t113i_nand.mk文件,修改前如下:
修改后如下:

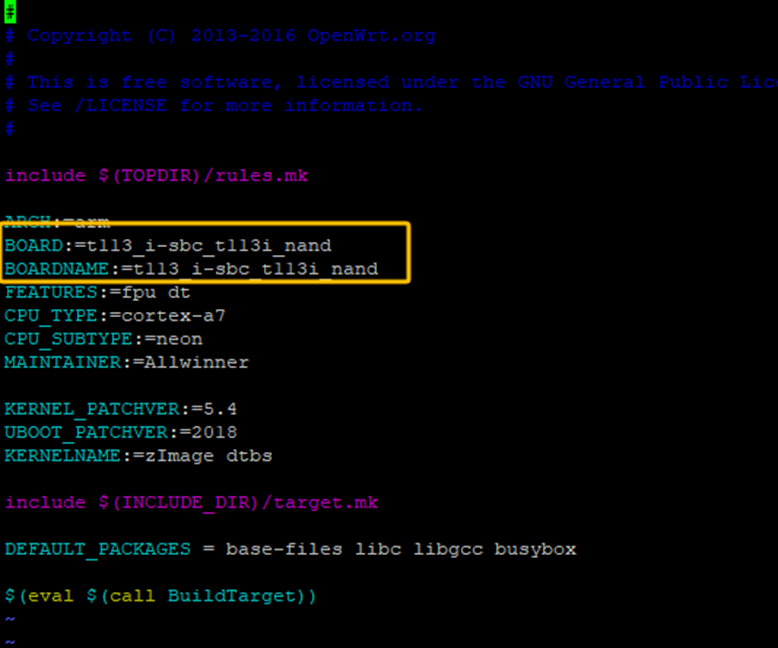
然后修改当前目录下的Makefile文件,修改前如下:
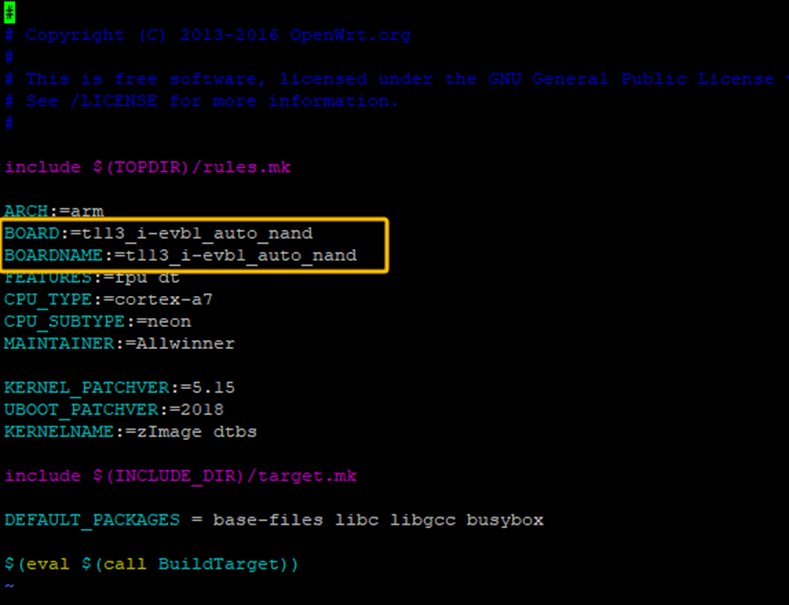
修改后如下:
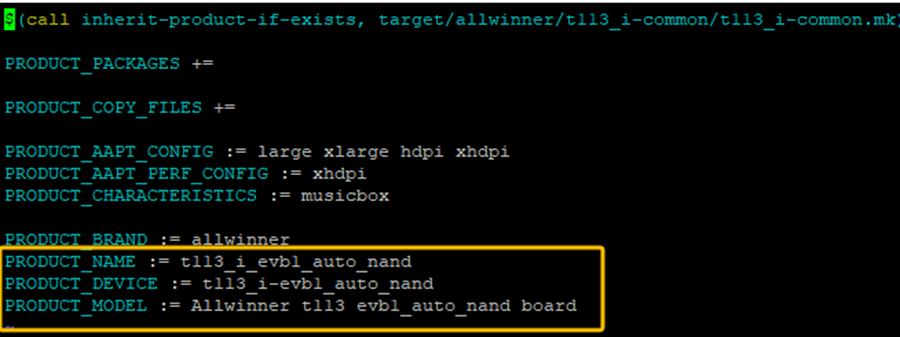
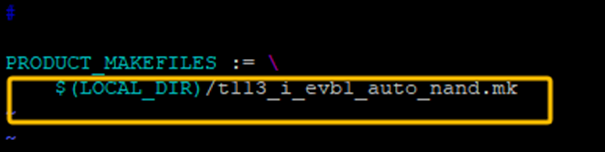
然后修改当前目录下的TinaProducts.mk文件,修改前如下:
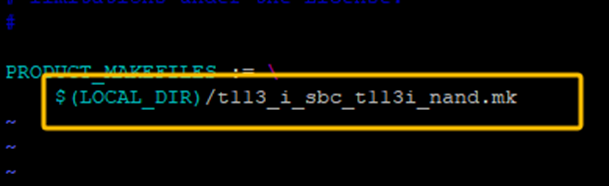
修改后如下:
然后修改defconfig文件,修改前如下:
修改后如下:

然后修改当前目录下的vendorsetup.sh文件,修改前如下:

修改后如下:

8.更新板卡编译配置信息
回到SDK的根目录
点击查看代码
source build/envsetup.sh
lunch
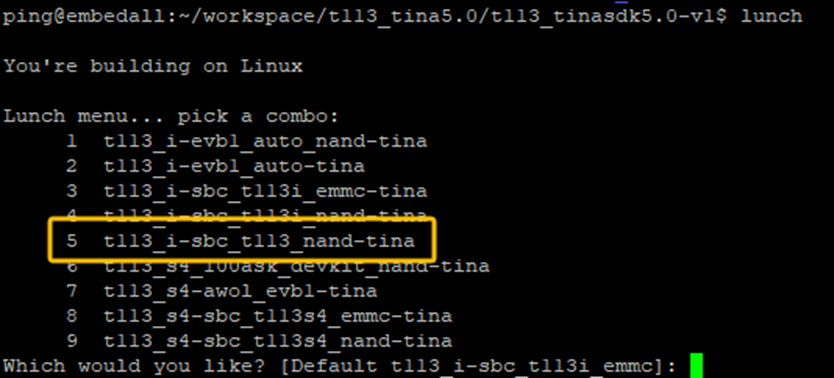
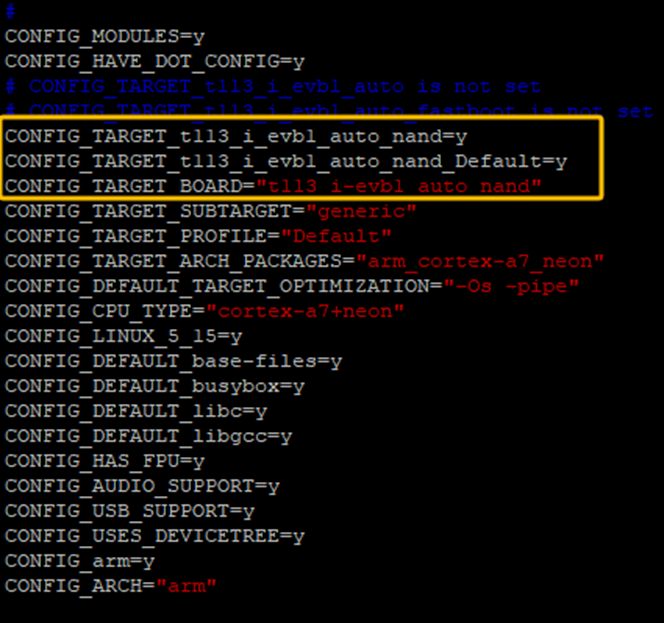
新加的平台已经添好了。选择5后,就会把根据该产品设备配置文件(BoardConfig.mk)对编译系统进行配置,配置后在SDK根目录生成.buildconfig文件。.buildconfig文件内容如下:
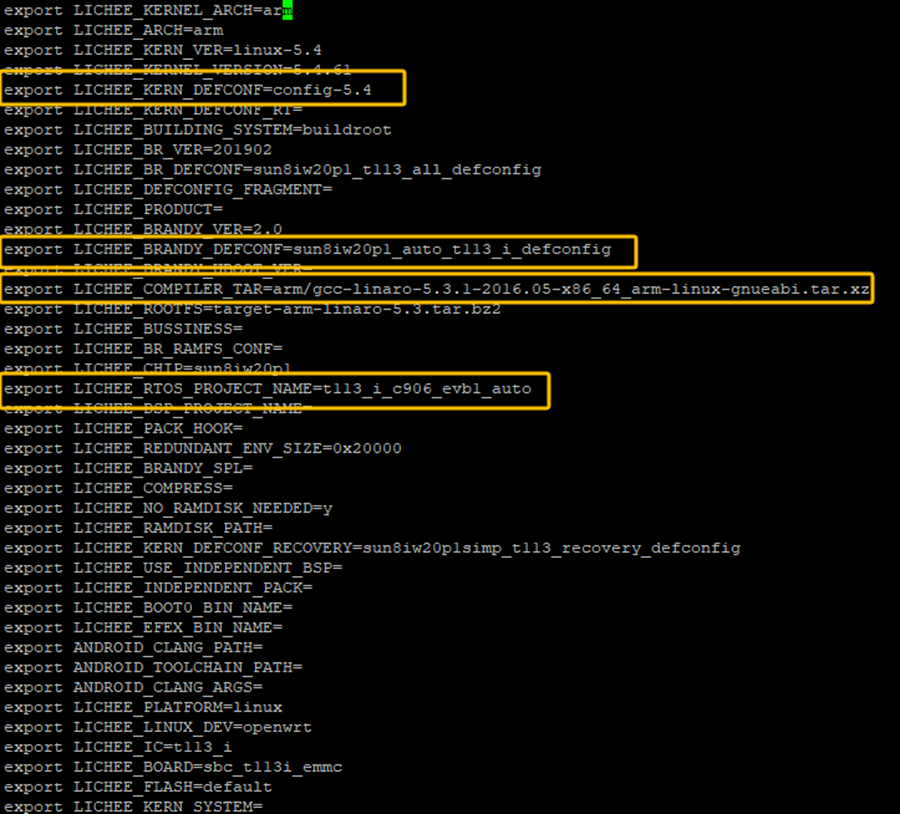
画黄色框的配置就是在BoardConfig.mk中配置的。如果BoardConfig.mk进行了修改,那务必重新lunch以适配新的编译环境。
